Tukukkk

Em matemática (especialmente topologia algébrica e álgebra abstrata), homologia (em parte do Grego ὁμός homos "identical") é uma maneira geral de associar uma sequência de objetos algébricos tais como grupos ou grupos abelianos ou módulos a outros objetos matemáticos tais como o espaço topológico. Na linguagem da teoria das categorias, dizemos que uma teoria de homologia é um functor covariante da categoria dos espaços topológicos na categoria dos grupos abelianos graduados. Grupos de homologia foram originalmente definidos em topologia algébrica. No entanto, construções semelhantes estão disponíveis em uma ampla variedade de outros contextos, tais como grupos, álgebra de Lie, Teoria de Galois e geometria algébrica.

Já em álgebra comutativa, uma teoria de homologia é um functor covariante da categoria dos complexos de cadeia na categoria dos grupos abelianos graduados. A álgebra homológica trata do estudo de tais functores. Além disto, existe dentro da teoria de categorias uma área de pesquisa denominada álgebra homológica abstrata,^[1] que generaliza as ferramentas da álgebra homológica ao contexto das categorias abelianas. Tal formulação da homologia algébrica foi concebida por A. Grothendieck para estudar feixes sobre variedades algébricas.^[2]

A motivação original para a definição de grupos de homologia foi a observação de que duas formas podem ser distinguidas examinando seus buracos. Por exemplo, um círculo não é um disco porque o círculo tem um furo através dele enquanto o disco é sólido, e a esfera ordinária não é um círculo porque a esfera delimita um furo bidimensional enquanto o círculo delimita um furo unidimensional. No entanto, porque um buraco é "não existente", não é imediatamente óbvio como definir um buraco ou como distinguir diferentes tipos de buracos. Homologia foi originalmente um método matemático rigoroso para definir e categorizar os buracos em uma variedade. Falando superficialmente, um "círculo" é uma subvariedade fechada, uma "fronteira" é a fronteira de uma subvariedade com limite e uma "classe de homologia" (que representa um buraco) é uma classe de equivalência de círculo módulo limites.

Existem muitas teorias de homologia diferentes. Um tipo particular de objeto matemático, como um espaço topológico ou um grupo, pode ter uma ou mais teorias de homologia associadas. Quando o objeto subjacente tem uma interpretação geométrica como os espaços topológicos, o n - grupo de homologia representa um comportamento exclusivo de dimensão n . Em geral, a maioria dos grupos de homologia ou módulos surgem como funtor derivado na apropriada categorias abelianas. Eles fornecem descrições concretas da falha de um functor para ser funtor exato. A partir desta perspectiva abstrata, os grupos de homologia são determinados por objetos de uma categoria derivada.

Background |

Origens |

Pode-se dizer que a teoria da homologia começa com a fórmula do poliedro de Euler, ou característica de Euler.^[3] Isto foi seguido pela definição de Riemann para genus e invariantes numéricos da conectividade do "n" - fold em 1857 e a prova de Betti em 1871 da independência de "números da homologia" da escolha da base.^[4]

A própria homologia foi desenvolvida como uma forma de analisar e classificar as variedades de acordo com seus "círculos" - laços fechados (ou mais geralmente subvariedades) que podem ser desenhados em uma dada variedade "n" - dimensional, mas não continuamente deformados um no outro.^[5] Estes círculos também são por vezes considerados como cortes que podem ser colados de volta juntos, ou como zíperes que podem ser presos e desatados. Os círculos são classificados por dimensão. Por exemplo, uma linha desenhada sobre uma superfície representa um 1-círculo, um laço fechado ou S1{displaystyle S^{1}} (1-variedade), enquanto uma superfície cortada através de uma variedade tridimensional é um 2-círculo.

Superfícies |

Círculos sobre uma 2-esfera

Na esfera S2{displaystyle S^{2}}, o ciclo b no diagrama pode ser encolhido para o pólo e até mesmo o círculo equatorial grande círculo a pode ser encolhido da mesma maneira. O teorema da curva de Jordan mostra que qualquer círculo arbitrário tal como c pode ser encolhido de forma semelhante até um ponto. Todos os círculos na esfera podem portanto ser continuamente transformados um no outro e pertencerem à mesma classe de homologia. Diz-se que eles são homólogos a zero. Cortar uma variedade ao longo de um círculo homólogo a zero separa a variedade em duas ou mais componentes. Por exemplo, cortar a esfera ao longo de a produz dois hemisférios.

Círculos sobre um toro

Isto não é geralmente verdade para círculos em outras superfícies. O toro T2{displaystyle T^{2}} tem círculos que não podem ser continuamente deformados um no outro, por exemplo no diagrama nenhum dos ciclos a , b ou c podem ser continuamente deformados um no outro. Os círculos a e b não podem ser reduzidos significativamente. Círculos c pode ser encolhido até um ponto, portanto é homólogo a zero.

Se a superfície do toro é cortada ao longo de ambos a e b, ele pode ser aberto e achatado em um retângulo ou, mais convenientemente, um quadrado. Um par de lados opostos representa o corte ao longo de a , e o outro par oposto representa o corte ao longo de b .

As bordas do quadrado podem então ser coladas de volta de diferentes maneiras. O quadrado pode ser torcido para permitir que as arestas se encontrem na direção oposta, como mostrado pelas setas no diagrama. Até a simetria, existem quatro maneiras distintas de colar os lados, cada um criando uma superfície diferente:

As quatro maneiras de colar um quadrado para fazer uma superfície fechada: cola setas simples juntos e cola setas duplas juntos.

Círculos sobre uma garrafa de Klein

K2{displaystyle K^{2}} é a garrafa de Klein, que é um toro com uma torção nele (a torção pode ser visto no diagrama quadrado como a inversão da seta em um dos lados). É um teorema que a superfície re-colada pode ter auto-interseção (quando imerso em 3-espaço Euclidiano). Como no toro, os círculos a e b não podem ser reduzidos enquanto c pode ser. Mas ao contrário do toro, seguindo o b avança para a direita e vice-versa para a esquerda e para a direita, porque b passa a cruzar a torção dada a uma junção. Se um corte equidistante de um lado de b for feito, ele retorna do outro lado e volta pela superfície uma segunda vez antes de retornar ao seu ponto de partida, cortando uma faixa de Möbius torcida. Como a esquerda e a direita locais podem ser arbitrariamente reorientadas dessa maneira, a superfície como um todo é dita não-orientável.

Círculos sobre o plano projetivo hemisférico

O plano projetivo P2{displaystyle P^{2}} tem ambas as colagens "torcidas". A forma não cortada, geralmente representada como a superfície do menino, é visualmente complexa, de modo que uma inserção hemisférica é mostrada no diagrama, em que os pontos antipodais ao redor da borda, como A e A', são identificados como o mesmo ponto. Novamente, a e b são não-reduzíveis enquanto c é. Mas desta vez, ambos a e b invertem à esquerda e à direita.

Círculos podem ser colados juntos, como foram a e b no toro quando foi cortado aberto e achatado para baixo. No diagrama da garrafa de Klein, a vai em uma direção e −a vai ao contrário. Se a é pensado como um corte, então −a pode ser pensado como uma operação de colagem. Fazendo um corte e, em seguida, re-colagem não muda a superfície, então a + (−a) = 0.

Seguindo um círculo orientável tal como a cerca de duas vezes dá simplesmente a + a = 2a . Mas círculos não-orientáveis se comportam de forma diferente. No plano projetivo, seguindo o círculo não-reduzível b contornando duas vezes notavelmente cria um círculo trivial que "pode" ser reduzido a um ponto; isto é, b + b = 0. Porque b deve ser seguido em torno de duas vezes para atingir um círculo zero, neste caso dizemos que a superfície tem um coeficiente de torção 2. O mesmo se aplica a b no exemplo da garrafa Klein. Para ver isso, você pode usar Teorema da curva de Jordan novamente.

Um quadrado é um espaço topológico contrátil, o que implica que tem homologia trivial. Consequentemente, cortes adicionais o deixa desconexo. O quadrado não é a única forma plana que pode ter os lados colados para gerar uma superfície. Colar os lados opostos de um octógono, por exemplo, produz uma superfície com dois furos. De fato, todas as superfícies fechadas podem ser produzidas colando os lados de algum polígono e todos os polígonos de lados pares (2n - lados) podem ser colados para formar superfícies diferentes. Por outro lado, uma superfície fechada com n não-nulas classe pode ser cortada em um 2n -lados. Também são possíveis variações, por exemplo, um hexágono também pode ser colado para formar um toro.^[6]

A primeira teoria reconhecível de homologia foi publicada por Henri Poincaré em seu paper seminal "Analysis situs", "J. Ecole polytech. (2) 1. 1-121 (1895). O artigo apresentou classes de homologia e relações. As possíveis configurações de círculos orientáveis são classificadas pelo número de Betti da variedade (os números de Betti são um refinamento da característica de Euler). A classificação dos círculos não-orientáveis requer informações adicionais sobre o coeficiente de torção. ^[5]

A classificação completa de 1- e 2-variedade é dada pela seguinte tabela:

Características topológicas de 1- e 2- variedades fechadas^[7]

Variedade		Número de Euler χ	Orientabilidade	Número de Betti			Coeficiente de torção (1-dimensional)
Símbolo[6]	Nome			b0	b1	b2
S1{displaystyle S^{1}}	Círculo (1-variedade)	0	Orientável	1	1	N/A	N/A
S2{displaystyle S^{2}}	Esfera	2	Orientável	1	0	1	nenhum
T2{displaystyle T^{2}}	Toro	0	Orientável	1	2	1	nenhum
P2{displaystyle P^{2}}	Plano projetivo	1	Não-orientável	1	0	0	2
K2{displaystyle K^{2}}	Garrafa de Klein	0	Não-orientável	1	1	0	2
	2-toro	−2	Orientável	1	4	1	nenhum
	g-toro (Genus = g)	2 − 2g	Orientável	1	2g	1	nenhum
	Esfera com c cross-caps	2 − c	Não-orientável	1	c − 1	0	2
	2-variedade com g buracos e c cross-caps (c > 0)	2 − (2g + c)	Não-orientável	1	(2g + c) − 1	0	2

NOTES:

1. Para uma superfície não-orientável, um buraco é equivalente a dois cross-caps.


2. Qualquer 2-variedade é uma soma conexa de um g-toro e c-planos projetivos. Para uma esfera S2{displaystyle S^{2}}, g = c = 0.

Generalização |

Uma variedade com bordo ou uma variedade aberta é topologicamente diferente de uma variedade fechada e pode ser criada fazendo um corte adequado em qualquer variedade fechada. Por exemplo, o disco ou 1-esfera B1{displaystyle B^{1}} é limitado por um círculo S1{displaystyle S^{1}}. Pode ser criado cortando um círculo trivial em qualquer 2-variedade e mantendo a peça removida, perfurando a esfera e esticando a punção de largura, ou cortando o plano projetivo. Também pode ser visto como preenchimento do círculo no plano.

Quando dois círculos podem ser continuamente deformados um no outro, então o corte ao longo de um produz a mesma forma que o corte ao longo do outro, até alguma flexão e alongamento. Neste caso, diz-se que os dois círculos são "homólogos" ou estão na mesma "classe de homologia". Adicionalmente, se um círculo puder ser continuamente deformado numa combinação de outros círculos, o corte ao longo do círculo inicial é o mesmo que o corte ao longo da combinação de outros círculos. Por exemplo, cortar ao longo de uma figura 8 é equivalente a cortar ao longo dos seus dois círculos. Neste caso, a figura 8 é dita homóloga à soma dos seus círculos.

Duas variedades abertas com bordas semelhantes (até alguma flexão e alongamento) podem ser colados em conjunto para formar uma nova variedade que é sua soma conexa.

Esta análise geométrica das variedades não é rigorosa. Em busca de maior rigor, Poincaré passou a desenvolver a homologia simplicial de uma variedade triangulada e criar o que agora é chamado de complexo de cadeia.^[8][9] Estes complexos de cadeia (desde muito generalizados) formam a base para a maioria dos tratamentos modernos de homologia.

Em tais tratamentos, um círculo não precisa ser contínuo: um 0-círculo é um conjunto de pontos, e o corte ao longo deste círculo corresponde à perfuração da variedade. Um 1-círculo corresponde a um conjunto de círculos fechados (uma imagem de uma 1-variedade S1{displaystyle S^{1}}). Em uma superfície, o corte ao longo de um círculo produz peças desconexas ou uma forma mais simples. Um 2-círculo corresponde a uma coleção de superfícies imersas, como uma esfera ou um toro, e assim por diante.

Emmy Noether e, independentemente, Leopold Vietoris e Walther Mayer desenvolveram a teoria dos grupos de homologia algébrica no período 1925-28.^[10][11][12] A nova topologia combinatória tratou formalmente as classes topológicas como o grupo abeliano. Grupos de homologia são grupos abelianos finitamente gerados, e classes de homologia são elementos desses grupos. Os números de Betti da variedade são a posição da parte livre do grupo de homologia, e os círculos não-orientáveis são descritos pela parte de torção. A subseqüente disseminação de grupos de homologia trouxe uma mudança de terminologia e ponto de vista de "topologia combinatória" para "topologia algébrica". ^[13] Homologia algébrica continua sendo o principal método de classificação de variedades.^[14]

Exemplos informais |

Informalmente, a homologia de um espaço topológico X é um conjunto dos invariantes topológicos de X representado por seus grupos de homologia

H0(X),H1(X),H2(X),…{displaystyle H_{0}(X),H_{1}(X),H_{2}(X),ldots }

Onde o kth{displaystyle k^{rm {th}}} grupo de homologia Hk(X){displaystyle H_{k}(X)} descreve os k -dimensionais buracos em X . Um buraco 0-dimensional é simplesmente um espaço entre duas componentes, conseqüentemente H0(X){displaystyle H_{0}(X)} descreve um caminho conexo em uma componentes de X .^[15]

O círculo ou 1-esfera S1{displaystyle S^{1}}

Uma esfera 1-dimensional S1{displaystyle S^{1}} é um círculo. Ele tem um único componente conexo e um furo unidimensional, mas sem furos de dimensão superior. Os grupos de homologia correspondentes são dados por

Hk(S1)={Zk=0,1{0}caso contrário{displaystyle H_{k}(S^{1})={begin{cases}mathbb {Z} &k=0,1\{0}&{text{caso contrário}}end{cases}}}

onde Z{displaystyle mathbb {Z} } é o grupo do inteiros e {0}{displaystyle {0}} é o grupo trivial. O grupo H1(S1)=Z{displaystyle H_{1}(S^{1})=mathbb {Z} } representa um grupo abeliano finitamente gerado, com um único gerador representando um buraco unidimensional contido em um círculo.^[16]

A 2-esfera S2{displaystyle S^{2}} é a casca, não o interior, de uma bola

Uma esfera bidimensional S2{displaystyle S^{2}} tem uma única componente conexa, sem buracos unidimensionais, um buraco bidimensional e sem buracos de dimensões maiores. Os grupos de homologia correspondentes são^[16]

Hk(S2)={Zk=0,2{0}caso contrário{displaystyle H_{k}(S^{2})={begin{cases}mathbb {Z} &k=0,2\{0}&{text{caso contrário}}end{cases}}}

Em geral para esferas n-dimensionais Sn{displaystyle S^{n}}, os grupos de homologia são:

Hk(Sn)={Zk=0,n{0}caso contrário{displaystyle H_{k}(S^{n})={begin{cases}mathbb {Z} &k=0,n\{0}&{text{caso contrário}}end{cases}}}

O disco sólido ou 1-bola B1{displaystyle B^{1}}

Uma bola unidimensional B1{displaystyle B^{1}} é um disco sólido. Ele tem uma única componente conexa por caminhos, mas em contraste com o círculo, não tem buracos unidimensionais ou de dimensões maiores. Os grupos de homologia correspondentes são todos triviais, exceto para H0(B1)=Z{displaystyle H_{0}(B^{1})=mathbb {Z} }. Em geral, para uma bola n-dimensional Bⁿ,^[16]

Hk(Bn)={Zk=0{0}caso contrário{displaystyle H_{k}(B^{n})={begin{cases}mathbb {Z} &k=0\{0}&{text{caso contrário}}end{cases}}}

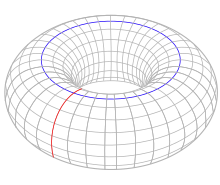
O toro T=S1×S1{displaystyle T=S^{1}times S^{1}}

O Toro é definido como o produto cartesiano de dois círculos T=S1×S1{displaystyle T=S^{1}times S^{1}}. O toro tem uma única componente conexa por caminhos, e dois buracos unidimensionais independentes (indicados pelos círculos vermelho e azul) e um buraco bidimensional como o interior do toro. Os grupos de homologia correspondentes são^[17]

Hk(T)={Zk=0,2Z×Zk=1{0}caso contrário{displaystyle H_{k}(T)={begin{cases}mathbb {Z} &k=0,2\mathbb {Z} times mathbb {Z} &k=1\{0}&{text{caso contrário}}end{cases}}}

Os dois buracos 1D independentes formam geradores independentes em um grupo abeliano finitamente gerado, expresso como o grupo de produtos cartesiano Z×Z{displaystyle mathbb {Z} times mathbb {Z} }.

Construção dos grupos de homologia |

Seja C{displaystyle {mathcal {C}}} um complexo de cadeias

…→An+1dn+1→Andn→An−1dn−1→An−2→…→A2d2→A1d1→A0d0→0.{displaystyle ldots to A_{n+1}{begin{matrix}d_{n+1}\to \,end{matrix}}A_{n}{begin{matrix}d_{n}\to \,end{matrix}}A_{n-1}{begin{matrix}d_{n-1}\to \,end{matrix}}A_{n-2}to ldots to A_{2}{begin{matrix}d_{2}\to \,end{matrix}}A_{1}{begin{matrix}d_{1}\to \,end{matrix}}A_{0}{begin{matrix}d_{0}\to \,end{matrix}}0.}

Definimos o n-ésimo grupo de homologia de C{displaystyle {mathcal {C}}} como Hn(C)=Nuc(dn)/Im(dn+1){displaystyle H_{n}({mathcal {C}})=Nuc(d_{n})/Im(d_{n+1}),}.

Já os grupos de homologia de um espaço topológico X{displaystyle X} são definidos a partir de um complexo de cadeia C(X){displaystyle C(X)} determinado por X{displaystyle X}. Um complexo de cadeia é uma sequência de grupos abelianos ou módulos C0,C1,C2,⋯{displaystyle C_{0},C_{1},C_{2},cdots }, conectados por um homomorfismos ∂n:Cn→Cn−1{displaystyle partial _{n}:C_{n}to C_{n-1}}, que são chamados de operadores limites.^[18] Isto é,

⋯⟶∂n+1Cn⟶∂nCn−1⟶∂n−1⋯⟶∂2C1⟶∂1C0⟶∂00{displaystyle dotsb {overset {partial _{n+1}}{longrightarrow ,}}C_{n}{overset {partial _{n}}{longrightarrow ,}}C_{n-1}{overset {partial _{n-1}}{longrightarrow ,}}dotsb {overset {partial _{2}}{longrightarrow ,}}C_{1}{overset {partial _{1}}{longrightarrow ,}}C_{0}{overset {partial _{0}}{longrightarrow ,}}0}

onde 0 denota o grupo trivial e Ci≡0{displaystyle C_{i}equiv 0} para i<0{displaystyle i<0}. Também é necessário que a composição de quaisquer dois operadores de fronteira consecutivos seja trivial. Isto é, para todos n,{displaystyle n,}

∂n∘∂n+1=0n+1,n−1,{displaystyle partial _{n}circ partial _{n+1}=0_{n+1,n-1},}

Isto é, a função constante enviando cada elemento de Cn+1{displaystyle C_{n+1}} para a identidade do grupo Cn−1{displaystyle C_{n-1}}. Que a fronteira de uma fronteira é trivial implica im(∂n+1)⊆ker⁡(∂n){displaystyle mathrm {im} (partial _{n+1})subseteq ker(partial _{n})}, onde im(∂n+1){displaystyle mathrm {im} (partial _{n+1})} denota a imagem de um operador de limitado e ker⁡(∂n){displaystyle ker(partial _{n})} seu núcleo. Elementos de Bn(X)=im(∂n+1){displaystyle B_{n}(X)=mathrm {im} (partial _{n+1})} são chamados de fronteira e elementos de Zn(X)=ker⁡(∂n){displaystyle Z_{n}(X)=ker(partial _{n})} são chamados de círculos.

Como cada grupo de cadeia Cn{displaystyle C_{n}} é abeliano todos os seus subgrupos são normais. Em seguida, porque im(∂n+1){displaystyle mathrm {im} (partial _{n+1})} e ker⁡(∂n){displaystyle ker(partial _{n})} são ambos subgrupos de Cn{displaystyle C_{n}}, im(∂n+1){displaystyle mathrm {im} (partial _{n+1})} é um subgrupo normal de ker⁡(∂n){displaystyle ker(partial _{n})}. Então, pode-se criar o grupo quociente

Hn(X):=ker⁡(∂n)/im(∂n+1)=Zn(X)/Bn(X),{displaystyle H_{n}(X):=ker(partial _{n})/mathrm {im} (partial _{n+1})=Z_{n}(X)/B_{n}(X),}

chamado de n-ésimo o grupo de homologia X{displaystyle X}. Os elementos de Hn(X){displaystyle H_{n}(X)} são chamados de classes de homologia. Cada classe de homologia é uma classe de equivalência de círculos, dois círculos que estão na mesma classe de homologia são considerados homólogos.^[19]

Um complexo de cadeia é dito ser exata se a imagem da (n + 1)-ésima função é sempre igual ao núcleo da n-ésima função. Os grupos de homologia de X{displaystyle X} medem, portanto, até que ponto o complexo de cadeia associado a X{displaystyle X} é exato.^[20]

Os grupos de homologia reduzidos de um complexo de cadeia C(X){displaystyle C(X)} são definidos como homologias do complexo de cadeia aumentada^[21]

⋯⟶∂n+1Cn⟶∂nCn−1⟶∂n−1⋯⟶∂2C1⟶∂1C0⟶ϵZ⟶0{displaystyle dotsb {overset {partial _{n+1}}{longrightarrow ,}}C_{n}{overset {partial _{n}}{longrightarrow ,}}C_{n-1}{overset {partial _{n-1}}{longrightarrow ,}}dotsb {overset {partial _{2}}{longrightarrow ,}}C_{1}{overset {partial _{1}}{longrightarrow ,}}C_{0}{overset {epsilon }{longrightarrow ,}}mathbb {Z} {longrightarrow ,}0}

onde o operador limite ϵ{displaystyle epsilon } é

ϵ(∑iniσi)=∑ini{displaystyle epsilon left(sum _{i}n_{i}sigma _{i}right)=sum _{i}n_{i}}

para a combinação ∑iniσi{displaystyle sum _{i}n_{i}sigma _{i}} dos pontos σi{displaystyle sigma _{i}}, os quais são geradores fixos de C0{displaystyle C_{0}}. Então o grupo de homologia reduzido H~i(X){displaystyle {tilde {H}}_{i}(X)} coincide com Hi(X){displaystyle H_{i}(X)} para i ≠ 0. O extra Z{displaystyle mathbb {Z} } no complexo de cadeia representa a única função [∅]⟶X{displaystyle [emptyset ]longrightarrow X} desde o simplexo vazio até o X{displaystyle X}.

Calcular os grupos do círculo Zn(X){displaystyle Z_{n}(X)} e da fronteira Bn(X){displaystyle B_{n}(X)} são geralmente bastante difíceis, pois têm um grande número de geradores. Por outro lado, existem ferramentas que facilitam a tarefa.

A homologia simplicial dos grupos Hn(X){displaystyle H_{n}(X)} de um complexo simplicial X{displaystyle X} é definido usando o complexo simplicial de cadeias C(X){displaystyle C(X)}, com Cn(X){displaystyle C_{n}(X)} o grupo abeliano livre gerado por um n-simplexo de X{displaystyle X}. Os grupos de homologia singular Hn(X){displaystyle H_{n}(X)} são definidos para qualquer espaço topológico X{displaystyle X}, e coincidem com os grupos de homologia simplicial para um complexo simplicial.

Os grupos de cohomologia são formalmente semelhantes aos grupos de homologia: um começamos com um complexo de co-cadeias, que é o mesmo que um complexo de cadeias, mas cujas setas, agora denotas por dn{displaystyle d^{n}}, apontam para a direção que n aumenta em vez de apontar para direção que n diminui; então os grupos ker⁡(dn)=Zn(X){displaystyle ker(d^{n})=Z^{n}(X)} de co-ciclos e im(dn−1)=Bn(X){displaystyle mathrm {im} (d^{n-1})=B^{n}(X)} de co-bordos seguem a mesma descrição. O n-ésimo grupo de cohomologia de X{displaystyle X} é então o grupo quociente.

Hn(X)=Zn(X)/Bn(X),{displaystyle H^{n}(X)=Z^{n}(X)/B^{n}(X),}

em analogia com o n-ésimo grupo de homologia.

As diversas maneiras de se associar um complexo de cadeias a um espaço topológico (ou por vezes, a um par de espaços topológicos), são chamadas de teorias de homologia. Algumas teorias de homologia para variedades diferenciáveis são: a homologia singular, a homologia de Čech, a homologia de Morse e a homologia de de Rham.

Tipos de homologia |

Os diferentes tipos de teoria de homologia surgem de funções de functores de várias categorias de objetos matemáticos para a categoria de complexos de cadeia. Em cada caso a composição do functor de objetos para complexos de cadeia e o functor de complexos de cadeia para grupos de homologia define o functor de homologia global para a teoria.^[22]

Homologia simplicial |

Ver artigo principal: Homologia Simplicial

O exemplo de motivação vem da topologia algébrica: a homologia simplicial de um complexo simplicial X. Aqui A_n é o grupo abeliano livre ou módulo cujos geradores são os simplexos orientados n-dimensionais de X. As funções são chamadas de mapeamentos de limites e enviam o simplexo com vértices

(a[0],a[1],…,a[n]){displaystyle (a[0],a[1],dots ,a[n])}

para a soma

∑i=0n(−1)i(a[0],…,a[i−1],a[i+1],…,a[n]){displaystyle sum _{i=0}^{n}(-1)^{i}left(a[0],dots ,a[i-1],a[i+1],dots ,a[n]right)}

(a qual é considerada 0 se n = 0).

Se considerarmos os módulos como sendo sobre um corpo, então a dimensão da n-ésima homologia de X resulta ser o número de "buracos" em X na dimensão n. Pode ser calculado pondo matriz representações destes mapeamentos de limite em forma normal de Smith.

Homologia Singular |

Ver artigo principal: Homologia Singular

Usando o exemplo de homologia simplicial como modelo, pode-se definir a homologia singular para qualquer espaço topológico X . Um complexo de cadeia para X é definido tomando A _n para ser o grupo abeliano livre (ou módulo livre) cujos geradores são todos funções contínuas de simplexos n-dimensionais em X . Os homomorfismos ∂n{displaystyle partial _{n}} surgem das funções limites de simplexos.

Grupo de homologia |

Ver artigo principal: Cohomologia de grupo

Em álgebra abstrata, usa-se homologia para definir functor derivada, por exemplo o funtor Tor. Aqui começa-se com algum functor covariante aditivo F e algum módulo X. O complexo de cadeia para X é definido como segue: primeiro encontre um módulo livre F1{displaystyle F_{1}} e um homomorfismo sobrejetivo p1:F1→X{displaystyle p_{1}:F_{1}to X}. Em seguida, encontra-se um módulo livre F2{displaystyle F_{2}} e um homomorfismo sobrejetivo p2:F2→ker(p1){displaystyle p_{2}:F_{2}to ker(p_{1})}. Continuando desta forma, pode ser definida uma sequência de módulos livres Fn{displaystyle F_{n}} e homomorfismos pn{displaystyle p_{n}}. Aplicando o funtor F a esta seqüência, obtém-se um complexo de cadeia; a homologia Hn{displaystyle H_{n}} deste complexo depende apenas de F e X e é, por definição, a n-derivada do funtor F, aplicado a X.

Outras teorias de homologia |

Homologia functors |

Os complexos de cadeia formam uma categoria: Um morfismo do complexo da cadeia dn:An→An−1{displaystyle d_{n}:A_{n}to A_{n-1}} para o complexo de cadeia en:Bn→Bn−1{displaystyle e_{n}:B_{n}to B_{n-1}} é uma seqüência de homomorfismos fn:An→Bn{displaystyle f_{n}:A_{n}to B_{n}} tal que fn−1∘dn=en∘fn{displaystyle f_{n-1}circ d_{n}=e_{n}circ f_{n}} para todo n. A n-ésima homologia Hn{displaystyle H_{n}} pode ser vista como um functor covariante da categoria de complexos de cadeia para a categoria de grupos abelianos (ou módulos).

Se o complexo da cadeia depende do objeto X de uma forma covariante (o que significa que qualquer morfismo X → Y induz um morfismo do complexo de cadeia de X ao complexo de cadeia de Y, então o H _n são functores covariantes da categoria em que X pertence à categoria de grupos abelianos (ou módulos).

A única diferença entre a homologia e a cohomologia é que, na cohomologia, os complexos de cadeia dependem de uma maneira contravariante em X, e que, portanto, os grupos de homologia (que são chamados de grupos de cohomologia neste contexto e denotado por Hⁿ) formam os functores contravariantes da categoria que X pertence à categoria de grupos abelianos ou módulos.

Propriedades |

Se (d_n: A_n → A_n-1) é um complexo de cadeia tal que todos mas finitamente muitos A_n são zero e os outros são grupos abelianos finamente gerados (ou espaços vetoriais de dimensão finita), então podemos definir a Característica de Euler

χ=∑(−1)nrank(An){displaystyle chi =sum (-1)^{n},mathrm {rank} (A_{n})}

(Usando a categoria no caso de grupos abelianos e a dimensão de Hamel no caso de espaços vetoriais). Acontece que a característica de Euler também pode ser calculada no nível de homologia:

χ=∑(−1)nrank(Hn){displaystyle chi =sum (-1)^{n},mathrm {rank} (H_{n})}

e, especialmente em topologia algébrica, isso fornece duas maneiras de calcular o invariante χ importante para o objeto X que deu origem ao complexo da cadeia.

Toda sequência exata curta

0→A→B→C→0{displaystyle 0rightarrow Arightarrow Brightarrow Crightarrow 0}

de complexos de cadeia origina uma sequência exata longa de grupos de homologia

⋯→Hn(A)→Hn(B)→Hn(C)→Hn−1(A)→Hn−1(B)→Hn−1(C)→Hn−2(A)→⋯{displaystyle cdots to H_{n}(A)to H_{n}(B)to H_{n}(C)to H_{n-1}(A)to H_{n-1}(B)to H_{n-1}(C)to H_{n-2}(A)to cdots }

Todos as funções nesta seqüência exata longa são induzidas pelos funções entre os complexos de cadeia, com exceção dos mapas H_n(C) → H_n-1(A) Estes últimos são chamados de homomorfismos conexos e são fornecidos pelo Lema de zig-zag. Este lema pode ser aplicado à homologia de várias maneiras que auxiliam no cálculo de grupos de homologia, tais como as teorias de homologia relativa e sequências de Mayer-Vietoris.

Aplicações |

Aplicação em matemática pura |

Os teoremas notáveis provados usando homologia incluem o seguinte:

• O Teorema do ponto fixo de Brouwer: Se f é uma função contínua qualquer de uma bola Bⁿ em si mesma, então existe um ponto fixo a ∈ Bⁿ com f(a) = a.


• 
  Invariância do domínio: Se U é um subconjunto aberto de Rⁿ e f : U → Rⁿ é uma função contínua injectiva, então V = f(U) é aberto e f é um homeomorfismo entre U e V.


• O Teorema da bola cabeluda: qualquer espaço vetorial sobre uma 2-esfera (ou mais geralmente, a 2k -esfera para qualquer k ≥ 1) é nula em algum ponto.


• O teorema de Borsuk-Ulam: qualquer função contínua de uma n-esfera no espaço Euclidiano n-dimensional conecta um par de pontos antipodal em um mesmo ponto. (Dois pontos em uma esfera são chamados antípodais se estiverem em direções exatamente opostas do centro da esfera.)

Aplicação em ciências e engenharia |

Na análise de dados topológicos, os conjuntos de dados são considerados como uma nuvem de pontos que é uma amostra da variedade ou variedade algébrica imersa no Espaço euclidiano. Ao ligar os pontos vizinhos mais próximos na nuvem em uma triangulação, é criada uma aproximação simplicial da variedade e sua homologia simplicial pode ser calculada. Encontrar técnicas para robustamente calcular a homologia usando várias estratégias de triangulação em várias escalas de comprimento é o tópico da homologia persistente.^[23]

Em rede de sensores, os sensores podem comunicar informações através de uma rede ad-hoc que muda dinamicamente no tempo. Para entender o contexto global deste conjunto de medições locais e caminhos de comunicação, é útil calcular a homologia da topologia de rede para avaliar, por exemplo, os buracos na cobertura.^[24]

Na teoria de sistemas dinâmicos em física, Poincaré foi um dos primeiros a considerar a interação entre a variedade invariante de um sistema dinâmico e seus invariantes topológicos. A teoria de Morse relaciona a dinâmica de um fluxo de gradiente em uma variedade com, por exemplo, sua homologia. A homologia de Floer estendeu isto a variedades de dimensão infinita. O teorema de KAM estabeleceu que a órbita periódica pode seguir trajetórias complexas; em particular, podem formar tranças que podem ser investigadas usando a homologia de Floer.^[25]

Em uma classe de métodos de elementos finitos, Problema de valor sobre o contorno para equações diferenciais envolvendo o operador de Hodge-Laplace pode precisar ser resolvido topologicamente em domínios não triviais, por exemplo, em simulações electromagnética. Nestas simulações, a solução é auxiliada pela fixação da classe de cohomologia da solução com base nas condições de contorno escolhidas e na homologia do domínio. Os domínios FEM podem ser triangulados, a partir dos quais a homologia simplicial pode ser calculada.^[26][27]

Software |

Muitos pacotes de software foram desenvolvidos para efeitos de calcular os grupos de homologia de complexos de células finitas. Linbox é uma biblioteca C++ para executar operações de matriz rápida, incluindo forma normal de Smith; ele interage com ambos Gap e Maple. Chomp, CAPD :: Redhom e Perseus também são escritos em C++. Todos os três implementam algoritmos de pré-processamento com base na Equivalência de Homotopia Simples e Teoria Morse discreta para realizar reduções de preservação de homologia dos complexos de células de entrada antes de recorrer à álgebra matricial. Kenzo é escrito em Lisp, e além de homologia pode também ser usado para gerar apresentação de Homotopia grupos de complexos simpliciais finitos. Gmsh inclui a solução homológica para malhas de elementos finitos, que pode gerar bases para Cohomologia diretamente utilizáveis por software de elementos finitos.^[26]

Veja também |

A Wikipédia tem o portal: Matemática

• Número de Betti


• Espaço de ciclo


• Axiomas de Eilenberg–Steenrod


• Teoria de Co-homologia Extraordinária


• Álgebra homológica


• Conjecturas homológicas em álgebra comutativa


• Dimensão homológica (desambiguação)


• Teorema de Künneth


• 
  Lista de teorias de co-homologia - também tem a Lista de teorias de homologia
  


• Coeficiente de torção

Referências

Bibliografia |

• 
  Elon Lages Lima (2012). Homologia Básica. Rio de Janeiro, RJ: [s.n.] ISBN 9788524402869  Parâmetro desconhecido |colecção= ignorado (ajuda)
  


• 
  Cartan, Henri Paul and Eilenberg, Samuel (1956) Homological Algebra Princeton University Press, Princeton, NJ, OCLC 529171
  


• Eilenberg, Samuel and Moore, J. C. (1965) Foundations of relative homological algebra (Memoirs of the American Mathematical Society number 55) American Mathematical Society, Providence, R.I., OCLC 1361982
  


• Hatcher, A., (2002) Algebraic Topology Cambridge University Press, ISBN 0-521-79540-0. Detailed discussion of homology theories for simplicial complexes and manifolds, singular homology, etc.


• 
  Homology group at Encyclopaedia of Mathematics


• 
  Hilton, Peter (1988), «A Brief, Subjective History of Homology and Homotopy Theory in This Century», Mathematical Association of America, Mathematics Magazine, 60 (5): 282–291, JSTOR 2689545 
  


• 
  Teicher, M. (ed.) (1999), The Heritage of Emmy Noether, ISBN 978-0-19-851045-1, Israel Mathematical Conference Proceedings, Bar-Ilan University/American Mathematical Society/Oxford University Press, OCLC 223099225 
  


• 
  Homology (Topological space), PlanetMath.org.


• Richeson, D.; Euler's Gem: The Polyhedron Formula and the Birth of Topology, Princeton University (2008)


• Spanier, Edwin H. (1966). Algebraic Topology., Springer, p. 155,. ISBN 0-387-90646-0.


• Timothy Gowers, June Barrow-Green, Imre Leader (2010), The Princeton Companion to Mathematics., Princeton University Press, ISBN 9781400830398.


• 
  John Stillwell (1993), Classical Topology and Combinatorial Group Theory, Springer, doi:10.1007/978-1-4612-4372-4_6, ISBN 978-0-387-97970-0.


• Charles A. Weibel (1999), History of Homological Algebra, chapter 28 in the book History of Topology by I.M. James, Elsevier, ISBN 9780080534077.

Predefinição:Topologia