Tukukkk

Elétron
Estimativas teóricas da densidade do elétron para orbitais do átomo do hidrogênio.
Composição:	partícula elementar[1]
Família:	Férmion
Grupo:	Lépton
Geração:	Primeira
Interação:	Gravidade, eletromagnética, fraca
Símbolo(s):	e− , β−
Antipartícula:	Pósitron (também chamado de antielétron)
Teorizada:	Richard Laming (1838–1851),[2] G. Johnstone Stoney (1874) e outros.[3][4]
Descoberta:	J. J. Thomson (1897)[5]
Massa:	6969910938355999999♠9.10938356(11)×10−31 kg[6] 6996548579909069999♠5.48579909070(16)×10−4 u[6] [7003182288848450000♠1822.8884845(14)]−1 u[notas 1] 6999510998946099999♠0.5109989461(31) MeV/c2[6]
Decaimento de partícula:	estável ( > 7028659999999999999♠6.6×1028 anos[7])
Carga elétrica:	3018839782351300000♠−1 e[notas 2] 3018839782343500000♠−1.602176565(35)×10−19 C[6] 3009519679549000000♠−4.80320451(10)×10−10 esu
Momento magnético:	−1.00115965218076(27) μB[6]
Spin:	1⁄2

O elétron ^{(português brasileiro)} (eletrão ^{[português europeu]}, electrão ^{[português angolano]}) (do grego ήλεκτρον, élektron, "âmbar") é uma partícula subatômica, de símbolo e−
ou β−
, com carga elétrica negativa.^[8] Pertence à primeira geração da família dos léptons,^[9] e considera-se que são partículas elementares porque não possuem componentes conhecidos.^[1] A massa do elétron é aproximadamente 1/1836 da massa do próton.^[10] As propriedades quânticas do elétron incluem um momento angular intrínseco (spin) fracionário, o que significa que é um férmion. Portanto, dois elétrons não podem ocupar o mesmo estado quântico, de acordo com o princípio da exclusão de Pauli.^[9] Como toda matéria, possui propriedades de ondas e de corpúsculos: pode colidir com outras partículas, mas também pode ser difratado, assim como a luz. As propriedades ondulatórias dos elétrons são mais fáceis de se observar experimentalmente do que as de outras partículas como os nêutrons e prótons porque os elétrons têm uma massa menor e assim um comprimento de onda de Broglie maior.

Os elétrons desempenham um papel essencial em muitos fenômenos físicos, tais como a eletricidade, o magnetismo e a condutividade térmica. Os elétrons estão sujeitos à ação de três interações fundamentais da natureza: a gravidade, a força eletromagnética e a força fraca.^[11] Por ter carga elétrica, um elétron gera um campo elétrico em sua vizinhança. Quando se move em relação a um observador gera também um campo magnético. Campos eletromagnéticos externos afetam um elétron por meio da força de Lorentz. Elétrons irradiam energia na forma de fótons quando acelerados. Elétrons são também essenciais em muitas aplicações tecnológicas, tais como a eletrônica, a soldagem, os tubos de raios catódicos, a microscopia eletrônica, a radioterapia, os lasers, os detectores de radiação ionizante e os aceleradores de partículas.

Interações envolvendo elétrons e outras partículas subatômicas são de interesse da química e da física nuclear. A interação entre os prótons, localizados no núcleo atômico, e os elétrons por meio da força de Coulomb é responsável pela estrutura do átomo. As ligações químicas são devidas à troca ou compartilhamento de elétrons entre dois ou mais átomos.^[12] O filósofo natural Richard Laming foi o primeiro a teorizar o conceito de uma carga elétrica de quantidade indivisível para explicar as propriedades químicas dos átomos em 1838.^[3] O físico George Johnstone Stoney nomeou esta carga como ‘electron’ em 1891, enquanto que Joseph John Thomson e sua equipe identificaram a partícula em 1897.^[5][13][14] Os elétrons também podem participar em reações nucleares, tais como a nucleossíntese estelar, onde são conhecidos como partículas beta. Elétrons podem ser criados a partir do decaimento beta de isótopos radioativos e em colisões de alta energia, por exemplo quando os raios cósmicos entram na atmosfera terrestre. A antipartícula do elétron é denominada pósitron; tem muitas características idênticas às do elétron, mas sua carga elétrica é positiva. Quando um elétron colide com um pósitron, ambas as partículas são totalmente aniquiladas, produzindo fótons de raios gama.

História e descobrimento do elétron |

Os gregos antigos observaram que o âmbar atraía pequenos objetos quando friccionado com a lã. Junto com o raio, este fenômeno é uma das primeiras observações registradas com a eletricidade.^[15] Em seu tratado De Magnete, publicado em 1600, o cientista inglês William Gilbert cunhou o termo em neolatim electricus, para se referir a esta propriedade de atração de pequenos objetos após a fricção.^[16] Ambas as palavras elétrico e eletricidade são derivadas da forma latina ēlectrum (que também é a raiz para a liga metálica de mesmo nome), que veio da palavra grega para o âmbar, ἤλεκτρον (ēlektron).

No início do século XVII, Francis Hauksbee e Charles François du Fay descobriram de modo independente o que eles acreditavam ser dois tipos de eletricidade, uma gerada a partir da fricção do vidro, e a outra da fricção da resina de âmbar. A partir disto, Du Fay teorizou que a eletricidade consistia de dois fluidos elétricos, vítreo e resinoso, que são separados pela fricção e que se neutralizam quando combinados.^[17] Uma década depois, Benjamin Franklin propôs que a eletricidade não era constituída por dois tipos de fluidos elétricos, mas pelo mesmo fluido sob diferentes pressões. Ele deu a eles a nomenclatura atual de carga positiva e negativa.^[18] Franklin imaginou que os portadores de carga fossem positivos.^[19]

Entre 1838 e 1851, o filósofo britânico Richard Laming desenvolveu a ideia de que o átomo seria composto de um núcleo de matéria cercado por partículas subatômicas com carga elétrica unitária.^[2] No início de 1846, o físico William Weber postulou que a eletricidade era composta de cargas fluidas positivas e negativas e que a interação entre elas seria descrita pela lei do inverso do quadrado. Após estudar o fenômeno da eletrólise em 1874, o físico George Johnstone Stoney sugeriu a existência de uma "quantidade de eletricidade singular definida", a carga de um íon monovalente. Ele foi capaz de estimar o valor desta carga elementar e por meio da lei de Faraday da eletrólise.^[20] Entretanto, Stoney acreditava que essas cargas estariam permanentemente ligadas aos átomos e que não poderiam ser removidas. Em 1881, o físico Hermann von Helmholtz argumentou que tanto as cargas negativas quanto as positivas seriam subdivididas em partes elementares que "comportam-se como átomos de eletricidade".^[3]

Em 1881, Stoney criou o termo electrolion, mas dez anos depois adotou a palavra electron para descrever estas cargas elementares, escrevendo em 1894: "... uma estimativa foi feita para o valor correto dessa unidade fundamental notável, para a qual eu tenho desde então ousado sugerir o nome electron.^{[notas 3]} Em 1906, uma proposta para mudar a nomenclatura para electrion não foi bem sucedida porque Hendrik Lorentz preferiu manter a palavra electron.^[21][22] A palavra inglesa electron é uma combinação das palavras electric e ion.^[23][24] O sufixo -on passou então a ser utilizado no nome de outras partículas subatômicas, tais como proton e neutron.^[25][26]

Descoberta |

Um raio de elétrons defletidos em um círculo por um campo magnético.^[27]

Em 1869, o físico Johann Wilhelm Hittorf estudava a condutividade elétrica em gases rarefeitos e descobriu um brilho emitido do cátodo que aumentava em tamanho com a redução da pressão do gás. Em 1876, o físico Eugen Goldstein demonstrou que os raios deste brilho formavam uma sombra, e os apelidou de raios catódicos.^[28] Durante a década de 1870, o físico e químico Sir William Crookes desenvolveu o primeiro tubo de raios catódicos com um vácuo no interior.^[29] Ele então demonstrou que os raios luminescentes aparecendo dentro do tubo carregavam energia e se moviam do cátodo para o ânodo. Além disso, ao aplicar um campo magnético, ele foi capaz de defletir os raios, assim demonstrando que os raios se comportavam como se fossem carregados negativamente.^[30][31] Em 1879, propôs que estas propriedades poderiam ser explicadas pelo que ele denominou 'matéria radiante'. Ele então sugeriu que este seria o quarto estado da matéria, consistindo de moléculas carregadas negativamente que eram projetadas com alta velocidade a partir do cátodo.^[32]

O físico Arthur Schuster realizou um experimento similar ao de Crookes, colocando placas de metal paralelas aos raios catódicos e aplicando um potencial elétrico entre as placas. O campo defletia os raios em direção a placa carregada positivamente, fornecendo maiores evidências que os raios carregavam cargas negativas. Através da medição da quantidade de deflecção para um dado nível de corrente elétrica, em 1890, Schuster foi capaz de estimar a relação massa-para-carga dos componentes dos raios. Todavia, isto resultou em um valor que era mais de mil vezes superior ao que era esperado, então foi dado pouco crédito aos seus cálculos na época.^[30][33]

Em 1892, Hendrik Lorentz sugeriu que a massa destas partículas (elétrons) poderia ser consequência de sua carga elétrica.^[34]

Em 1896, o físico J. J. Thomson, com seus colegas John S. Townsend e Harold A. Wilson,^[13] executaram experimentos indicando que os raios catódicos eram partículas únicas, aos invés de ondas, átomos ou moléculas como era acreditado anteriormente.^[5] Thomson fez boas estimativas tanto da carga e e da massa m, descobrindo que as partículas dos raios catódicos, que ele chamou de "corpúsculos", teriam talvez um milésimo da massa do menor íon conhecido: o hidrogênio.^[5][14] Ele demonstrou que a relação carga para massa, e/m, era independente do material do cátodo. Também demonstrou que as partículas carregadas negativamente produzidas por materiais radioativos, pelo aquecimento de materiais e pelos materiais luminosos eram universais.^[5][35] O nome electron foi novamente proposto para estas partículas pelo físico George Fitzgerald, e o nome então ganhou aceitação universal.^[30]

Robert Millikan

Enquanto estudava a fluorescência natural de minerais em 1896, o físico Henri Becquerel descobriu que eles emitiam radiação sem nenhuma exposição a uma fonte externa de energia. Estes materiais radioativos se tornaram o interesse de muitos cientistas, incluindo o físico Ernest Rutherford que descobriu que eles emitiam partículas. Ele denominou estas partículas como alfa e beta, com base na sua capacidade de penetrar a matéria.^[36] Em 1900, Becquerel demonstrou que os raios beta emitidos pelo rádio podiam ser defletidos por um campo elétrico, e que a relação massa-para-carga era a mesma que para os raios catódicos.^[37] Esta evidência fortaleceu a visão de que os elétrons existiam como componentes dos átomos.^[38][39]

A carga do elétron foi medida com mais cuidado pelos físicos Robert Millikan e Harvey Fletcher em sua experiência da gota de óleo de 1909. Este experimento usou um campo elétrico para prevenir uma gota de óleo carregada de cair pela ação da gravidade. Este dispositivo podia medir a carga elétrica de tão poucos íons quanto de 1 a 150, com uma margem de erro de menos de 0,3%. Experimentos comparáveis feitos anteriormente pela equipe de Thomson,^[5] utilizando nuvens de gotas de água carregadas geradas pela eletrólise,^[13] e em 1911 por Abram Ioffe, obtiveram de modo independente o mesmo resultado que Millikan usando micropartículas de metal carregadas, cujos resultados foram em 1913.^[40] Todavia, gotas de óleo eram mais estáveis do que de água por causa de sua baixa taxa de evaporação, e assim eram mais adequadas para a experimentação por longos períodos de tempo.^[41]

No início do século XX, foi descoberto que sob certas condições uma partícula carregada se movimentando rapidamente causava a condensação de vapor de água supersaturada ao longo do seu caminho. Em 1911, Charles Wilson empregou este princípio para criar a câmara de nuvens para que pudesse fotografar o caminhos destas partículas, tais como os elétrons em alta velocidade.^[42]

Teoria atômica |

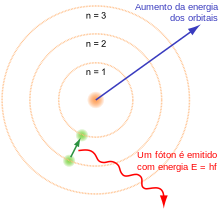
O Modelo atômico de Bohr, mostrando os estados dos elétrons com energia quantizada pelo número n. Um elétron caindo para as órbitas inferiores emite um fóton com a mesma energia entre os orbitais.

Em 1914, experimentos dos físicos Ernest Rutherford, Henry Moseley, James Franck e Gustav Hertz demonstraram amplamente a estrutura de um átomo como um núcleo de carga positiva cercado por elétrons de baixa massa.^[43] Em 1913, o físico Niels Bohr postulou que os elétrons residiam em estados de energia quantizada, com a energia determinada pelo momento angular das órbitas do elétron sobre o núcleo. Os elétrons poderiam se mover entre estes estados, ou órbitas, pela emissão ou absorção de fótons em frequências específicas. Por meio destas órbitas quantizadas, ele explicou com precisão as linhas espectrais do átomo de hidrogênio.^[44] Porém, o modelo de Bohr falhou em explicar a intensidade relativa das linhas espectrais e não foi bem sucedido em explicar o espectro de átomos mais complexos.^[43]

As ligações químicas entre átomos foram explicadas por Gilbert Newton Lewis, que em 1916 propôs que a ligação covalente entre dois átomos é mantida por um par de elétrons compartilhados entre eles.^[45] Posteriormente, em 1927, Walter Heitler e Fritz London deram uma explicação completa da formação do par de elétrons e a ligação química em termos de mecânica quântica.^[46] Em 1919, o químico Irving Langmuir elaborou o modelo estático de Lewis do átomo e sugeriu que todos os elétrons eram distribuídos em sucessivas "camadas esféricas (quase) concêntricas, de mesma espessura".^[47] As camadas eram, por sua vez, eram divididas em um número de células, cada uma contendo um par de elétrons. Com este modelo, Langmuir foi capaz de explicar qualitativamente as propriedades químicas de todos os elementos na tabela periódica,^[46] os quais já se sabia que se repetiam amplamente entre eles de acordo com a lei periódica.^[48]

Em 1924, o físico Wolfgang Pauli observou que a estrutura em forma de camada do átomo poderia se explicada por um conjunto de quatro parâmetros que definiriam cada estado de energia quântica, enquanto cada estado fosse inabitado por não mais que um único elétron. (Esta proibição contra mais de um elétron ocupando o mesmo estado de energia quântica ficou conhecida como princípio da exclusão de Pauli.)^[49] O mecanismo físico para explicar o quarto parâmetro, que tinha dois valores possíveis distintos, foi elaborado pelos físicos Samuel Goudsmit e George Uhlenbeck. Em 1925, Goudsmit e Uhlenbeck sugeriram que um elétron, além do momento angular de sua órbita, possuía um momento angular intrínseco e momento dipolo magnético.^[43][50] O momento angular intrínseco ficou conhecido como spin e explicou a divisão misteriosa das linhas espectrais observadas em espectrômetros de alta resolução; este fenômeno ficou conhecido como divisão da estrutura fina.^[51]

Mecânica quântica |

Em sua dissertação Recherches sur la théorie des quanta (Pesquisa na Teoria Quântica), o físico Louis de Broglie teorizou que toda a matéria possuia uma onda de matéria similar à luz.^[52] Isto é, sob condições apropriadas, elétrons e outras matérias iriam demonstrar propriedades tanto de partículas como de ondas. As propriedades corpusculares de uma partícula são demonstradas quando apresentam uma posição localizada no espaço ao longo de sua trajetória em um dado momento.^[53] A natureza similar às ondas é observada, por exemplo, quando um raio de luz passa através de fendas paralelas e cria padrões de interferência. Em 1927, o efeito da interferência foi observado em um raio de elétrons pelo físico George Paget Thomson com um filme de metal fino e pelos físicos Clinton Davisson e Lester Germer usando um cristal de níquel.^[54]

Na mecânica quântica, o comportamento do elétron em um átomo é descrito por um orbital atômico, que é a probabilidade de distribuição ao invés de uma órbita. Na figura, as sombras indicam a probabilidade relativa de "encontrar" um elétron, dada a energia correspondente para um número quântico, naquele ponto.

A previsão de De Broglie da natureza de onda para os elétrons levou a Erwin Schrödinger postular uma equação de onda para os elétrons se movendo sob a influência do núcleo do átomo. Em 1926, esta equação, a equação de Schrödinger, descreveu com sucesso como os elétrons se propagam.^[55]

Ao invés de produzir uma solução que determinava a localização de um elétron ao longo do tempo, esta equação também poderia ser usada para predizer a probabilidade de encontrar um elétron perto de uma posição, especialmente uma posição perto de onde o elétron estava ligado no espaço, para o qual a equação de onda do elétron não mudava ao longo do tempo. Esta abordagem levou a segunda formulação da mecânica quântica (a primeira sendo de Heisenberg em 1925), e as soluções da equação de Schrödinger, assim como de Heisenberg, forneceram derivações para os estados energéticos de um elétron em um átomo de hidrogênio que eram equivalentes a aqueles que tinham sido fornecidos inicialmente por Bohr em 1913, e que eram conhecidos por reproduzir o espectro do hidrogênio.^[56] Depois que o spin e a interação de múltiplos elétrons foi considerada, a mecânica quântica posteriormente tornou possível predizer a configuração dos elétrons nos átomos com números atômicos maiores que do hidrogênio.^[57]

Em 1928, baseado no trabalho de Wolfgang Pauli, Paul Dirac desenvolveu um modelo para o elétron – a equação de Dirac, consistente com a teoria da relatividade, pela aplicação das considerações de simetria e relativística para a formulação do Hamiltoniano da mecânica quântica no campo eletromagnético.^[58] Para resolver alguns problemas com sua equação relativística, em 1930 Dirac desenvolveu um modelo de um vácuo como um mar infinito de partículas tendo energia negativa, que foi apelidado de mar de Dirac. Isto o levou a predizer a existência de um pósitron, uma contraparte de anti-matéria do elétron.^[59] Esta partícula foi descoberta em 1932 por Carl Anderson, que sugeriu chamar os elétrons padrões de negatrons, e usar o elétron como um termo genérico para descrever ambas as variantes carregadas negativamente e positivamente.

Em 1947, Willis Lamb, em colaboração com Robert Retherford, descobriu que certos estados quânticos do átomo de hidrogênio, que deveriam ter a mesma energia, eram deslocados em relação ao outro, a diferença sendo o desvio de Lamb. Na mesma época, Polykarp Kusch, trabalhando com Henry M. Foley, descobriu que o momento magnético do elétron é levemente superior ao previsto pela teoria de Dirac. Esta pequena diferença foi posteriormente chamada de momento dipolo magnético anômalo do elétron. Posteriormente, tal diferença foi explicada pela teoria da eletrodinâmica quântica, desenvolvida por Sin-Itiro Tomonaga, Julian Schwinger e Richard Feynman no final da década de 1940.^[60]

Aceleradores de partículas |

Com o desenvolvimento do acelerador de partículas durante a primeira metade do século XX, os físicos começaram a estudar em profundidade as propriedades das partículas subatômicas.^[61]

A primeira tentativa bem sucedida de acelerar elétrons usando a indução eletromagnética foi feita em 1942 por Donald Kerst. Seu betatron inicial alcançou a energia de 2,3 MeV, enquanto betatrons subsequentes alcançaram 300 MeV. Em 1947, a radiação síncrotron foi descoberta com um elétron síncroton de 70 MeV pela General Electric. Esta radiação foi causada pela aceleração de elétrons, movendo-se próximos a velocidade da luz através do campo magnético^[62]

Com um raio de energia de 1,5 GeV, o primeiro colisor de partículas de alta energia foi o ADONE, que iniciou sua operação em 1968.^[63]

Este dispositivo acelerou elétrons e pósitrons em direções opostas, efetivamente dobrando a energia de suas colisões quando comparadas com a colisão de um alvo estático com um elétron.^[64] O Grande Colisor de Elétrons e Pósitrons da Organização Europeia para a Pesquisa Nuclear, que esteve operacional entre 1989 e 2000, alcançou colisões energéticas de 209 GeV e fez importantes medições para o Modelo Padrão da física de partículas.^[65][66]

Características |

Classificação |

Modelo padrão de partículas elementares. O elétron (símbolo e) está na esquerda.

No modelo padrão da física de partículas, os elétrons pertencem ao grupo de partículas subatômicas chamadas de léptons, o qual se acredita ser uma partícula elementar ou fundamental. Os elétrons tem a menor massa de um lépton carregado (ou partícula eletricamente carregada de qualquer tipo) e pertencem à primeira geração de partículas fundamentais.^[67] A segunda e a terceira gerações contêm léptons carregados, o múon e o tau, que são idênticos ao elétron em carga, spin e interações fundamentais, porém são mais massivos. Léptons diferem dos outros constituintes básicos das matérias, os quarks, por não interagirem por meio da força forte. Todos os membros do grupo dos léptons são férmions, porque todos eles possuem um spin fracionário; o elétron tem um spin de 12.^[68]

Propriedades fundamentais |

A massa invariante de um elétron é aproxidamente de 6969910900000000000♠9.109×10⁻³¹ kilogramas,^[69] ou 6996548900000000000♠5.489×10⁻⁴ unidades de massa atômica. Com base no princípio de Einstein da equivalência massa-energia, esta massa corresponde a um resto de energia de 0.511 MeV. A razão entre a massa de um próton e a de um elétron é de aproximadamente 1836.^[10][70] Medições astronômicas demonstram que a proporção mássica entre o próton e o elétron tem mantido o mesmo valor por pelo menos a metade da idade do universo, conforme foi previsto pelo modelo padrão.^[71]

Elétrons têm uma carga elétrica de 3018839800000000000♠−1.602×10⁻¹⁹ Coulomb,^[69] que é utilizada como unidade padrão para a carga de partículas subatômicas, e também é chamada de carga elementar. Esta carga elementar tem uma incerteza relativa padrão de 6992220000000000000♠2.2×10⁻⁸.^[69] Dentro dos limites da precisão experimental, a carga do elétron é idêntica a do próton, porém com o sinal oposto.^[72] Uma vez que o símbolo e é utilizado para a carga elementar, o elétron é comumente simbolizado pelo e−
, no qual o sinal negativo indica a carga negativa. O pósitron é simbolizado pelo e+
porque tem as mesmas propriedades que o elétron porém com uma carga positiva ao invés da negativa.^[68][69]

O elétron tem um momento angular intrínseco ou spin de 12.^[69] Esta propriedade é normalmente estabelecida ao se referir ao elétron como uma partícula spin-12.^[68] Para tais partículas a magnitude do spin é √32 ħ.^{[notas 4]} enquanto o resultado de uma medição de uma projeção de um spin em qualquer eixo pode ser somente ±ħ2. Além do spin, o elétron tem um momento magnético ao longo do eixo giratório.^[69] É aproximadamente igual a um Magnetão de Bohr,^{[73][notas 5]} que é uma constante física de valor igual a 6976927400914999999♠9.27400915(23)×10⁻²⁴ joules por tesla.^[69] A orientação do spin com respeito ao momento do elétron define a propriedade das partículas elementares conhecida como helicidade.^[74]

O elétron não possui subestrutrutura conhecida.^[1][75] e assume-se ser um ponto material com uma carga pontual e nenhuma extensão espacial.^[9] Na física clássica, o momento angular e o momento magnético de um objeto dependem de suas dimensões físicas. Consequentemente, o conceito de um elétron sem dimensões possuir estas propriedades não está de acordo com observações experimentais em armadilhas de Penning que indicam o elétron com um raio finito e não-nulo. Uma possível explicação para esta situação paradoxal é descrita abaixo na subseção "Partículas virtuais" ao levar em consideração a transformação Foldy–Wouthuysen.

O problema do raio do elétron é um desafio para a física teórica moderna. A admissão da hipótese de um raio finito de um elétron é incompatível com as premissas da teoria da relatividade. Por outro lado, um elétron como um ponto (raio zero) gera dificuldades matemáticas sérias devido a auto-energia do elétron tender ao infinito.^[76]

A observação de um único elétron em uma armadilha de Penning demonstra que o limite superior do raio da partícula é de 10⁻²² metros.^[77]

Também há uma constante física chamada de raio clássico do elétron, com um valor muito maior de 6985281789999999999♠2.8179×10⁻¹⁵ m, maior inclusive que o raio do próton. Entretanto, a terminologia provém de um cálculo simplista que ignora os efeitos da mecânica quântica; na realidade o raio clássico do elétron tem pouco a ver com a verdadeira estrutura fundamental do elétron.^{[78][notas 6]}

Existem partículas elementares que espontaneamente decaem em partículas menos massivas. Um exemplo é o múon, que decai para um elétron, um neutrino e um antineutrino, com um tempo de meia-vida de 6994220000000000000♠2.2×10⁻⁶ segundos. Todavia, acredita-se que o elétron é estável no fundamento teórico: o elétron é a partícula menos massiva com uma carga elétrica diferente de zero, então seu decaimento iria violar a conservação de carga.^[79] O limite experimental inferior para o tempo de meia vida do elétron é de 7028659999999999999♠6.6×10²⁸ anos, com um intervalo de confiança de 90%.^[7][80][81]

Propriedades quânticas |

Assim como todas as outras partículas, os elétrons podem se comportar como ondas. Esta propriedade é denominada dualidade onda-corpúsculo e pode ser demonstrada utilizando a experiência da dupla fenda.

A natureza ondulatória do elétron permite que ele passe através de duas fendas paralelas, ao invés de passar somente por uma, como seria esperado para uma partícula clássica. Na mecânica quântica, a propriedade ondulatória de uma partícula pode ser descrita matematicamente como uma função complexa, denominada função de onda, comumente representada pela letra grega psi (ψ).^[82][83]

Exemplo de uma função de onda antissimétrica para um estado quântico de dois férmions idênticos em uma caixa unidimensional. Se as partículas mudarem de posição, a função de onda inverte seu sinal.

Elétrons são partículas idênticas porque não podem ser distinguidas uma das outras devido a suas propriedades físicas intrínsecas. Na mecânica quântica, isto significa que um par de elétrons interagindo deve ser capaz de mudar de posições sem uma mudança observável para o estado do sistema. A função de onda de férmions, incluindo elétrons, é antisimétrica, o que significa que pode mudar de sinal quando dois elétrons são trocados; isto é ψ(r₁, r₂) = −ψ(r₂, r₁), onde as variáveis r₁ e r₂ correspondem ao primeiro e segundo elétrons, respectivamente. Uma vez que o valor absoluto não é alterado pelo sinal na troca, isto corresponde a probabilidades idênticas. Bósons, tais como o próton, tem funções de onda simétricas.^[82][83]

No caso da antisimetria, soluções para a equação de onda para elétrons interagindo resulta em uma probabilidade zero de que cada par ocupe o mesmo local ou estado. Isto é responsável pelo princípio da exclusão de Pauli, que impede que dois elétrons de ocupar o mesmo estado quântico. Este princípio explica muitas das propriedades dos elétrons. Por exemplo, isto provoca que grupos de elétrons ligantes ocupem orbitais diferentes em um átomo, ao invés de se sobreporem num mesmo orbital.^[82][83]

Partícula virtual |

Em uma visão simplificada, cada fóton passa algum tempo como uma combinação de um elétron virtual com sua antipartícula, o pósitron virtual, que rapidamente se aniquilam.^[84] A combinação da variação de energia necessária para criar estas partículas, e o tempo durante o qual elas existem, caem em um limiar de detectabilidade expressado pelo princípio da incerteza de Heisenberg, ΔE · Δt ≥ ħ. Como efeito, a energia necessária para criar estas partículas virtuais, ΔE, pode ser "emprestada" do vácuo quântico por um período de tempo, Δt, então seu produto não é mais do que a constante de Planck reduzida, ħ ≈ 6984660000000000000♠6.6×10⁻¹⁶ eV·s. Assim, para um elétron virtual, Δt é no máximo 6979129999999999999♠1.3×10⁻²¹ s.^[85]

Uma descrição esquemática do par virtual elétron-pósitron aparecendo aleatoriamente perto de um elétron (parte inferior à esquerda)

Enquanto um par virtual elétron-pósitron existe, a força de Coulomb do campo elétrico ambiente em volta de um elétron provoca um pósitron criado a ser atraído pelo elétron original, enquanto o elétron criado experimenta uma repulsão. Isto causa o que é chamado de polarização do vácuo. Como efeito, o vácuo se comporta como um meio tendo uma constante dielétrica maior que uma unidade. Assim a carga efetiva de um elétron é na verdade menor do que o seu valor verdadeiro, e a carga diminui com o aumento da distância do elétron.^[86][87] Esta polarização foi confirmada experimentalmente em 1997 utilizando o acelerador de partículas TRISTAN.^[88] Partículas virtuais causam um efeito de blindagem comparável para a massa do elétron.^[89]

A interação com partículas virtuais também explica o pequeno (na ordem de 0,1%) desvio do momento magnético intrínseco de um elétron para o do magneton de Bohr (a anomalia do momento magnético).^[73][90] O nível de concordância extraordinário entre a diferença prevista e a determinada experimentalmente é vista como uma das grandes realizações da eletrodinâmica quântica.^[91]

O paradoxo aparente (mencionado acima na subseção de propriedades) de uma partícula pontual tendo um momento angular intrínseco e momento magnético pode ser explicada pela formação de fótons virtuais no campo elétrico gerado pelo elétron. Estes fótons fazem o elétron mudar para um modo tremido (conhecido como zitterbewegung),^[92] que resulta em um movimento circular com precessão. Este movimento produz o spin e o momento magnético do elétron.^[9][93] Em átomos, esta criação de fótons virtuais explica o desvio de Lamb observado em linhas espectrais.^[86]

Interação |

Um elétron gera um campo elétrico que exerce uma força atrativa em uma partícula com carga positiva, tal como um próton, e uma força repulsiva em uma partícula negativa. A intensidade desta força é determinada pela lei do inverso do quadrado de Coulomb.^[94] Quando o elétron está em movimento, gera um campo magnético.^[82]:140 A lei de Ampére-Maxwell relaciona o campo elétrico a massa em movimento do elétron (a corrente elétrica) em relação a um observador. Esta propriedade de indução alimenta o campo magnético que move um motor elétrico.^[95] O campo eletromagnético de uma partícula carregada arbitrariamente em movimento é expresso pelo potencial de Liénard–Wiechert, o qual é válido mesmo quando a partícula está próxima da relativística da luz.

Uma partícula carregada q (à esquerda) está se movendo com velocidade v através do campo magnético B que está orientado em direção ao observador. Para um elétron, q é negativo então segue uma trajetória curva em direção ao topo.

Quando um elétron está se movendo através do campo magnético, está sujeito a força de Lorentz que atua perpendicularmente ao plano definido pelo campo magnético e a velocidade do elétron. Esta força centrípeta faz o elétron seguir uma trajetória helicoidal através do campo com um raio chamado de raio de Larmor. A aceleração deste movimento em curva induz um elétron a irradiar energia na forma de radiação síncrotron.^{[82]:160[96][notas 7]} A emissão de energia por sua vez provoca um recuo do elétron, conhecido como força Abraham–Lorentz, que cria uma fricção que retarda o elétron. Esta força é provocada pela “reação de volta” do próprio campo do elétron sobre si mesmo.^[97]

Os fótons mediam interações eletromagnéticas entre partículas na eletrodinâmica quântica. Um elétron isolado em uma velocidade constante não pode emitir ou absorver nenhum fóton real; ao fazê-lo iria violar a lei da conservação da energia e o momento linear. Por outro lado, fótons virtuais podem transferir momento entre duas partículas carregadas. Esta troca de fótons virtuais, por exemplo, gera a força Coulomb.^[98] A emissão de energia pode ocorrer quando um elétron em movimento é defletido por uma partícula carregada, tal como um próton. A aceleração do elétron resulta na emissão da radiação Bremsstrahlung.^[99]

Aqui, a radiação Bremsstrahlung é produzida por um elétron e defletido por um campo elétrico de um núcleo atômico. A mudança de energia E₂ − E₁ determina a frequência f do fóton emitido.

Uma colisão inelástica entre um fóton (luz) e um elétron solitário (livre) é chamada de efeito Compton. Esta colisão resulta na transferência de momento e energia entre as partículas, o que modifica o comprimento de onda do fóton em um valor chamado de desvio de Compton.^{[notas 8]} A magnitude máxima do desvio do comprimento de onda é h/m_ec, que é conhecido como comprimento de onda Compton.^[100] Para um elétron, tem uma valor de 6988243000000000000♠2.43×10⁻¹² m.^[69] Quando o comprimento de onda da luz é longo (por exemplo, o comprimento de onda da luz visível é 0.4–0.7 μm) o desvio do comprimento de onda se torna desprezível. Tal interação entre a luz e elétrons livres é chamada de efeito Thomson ou efeito Thomson linear.^[101]

A força relativa da interação eletromagnética entre duas partículas carregadas, tais como um elétron e um próton, é dada pela constante de estrutura fina. Este valor é uma quantidade adimensional formada pela razão das duas energias: a energia eletrostática de atração (ou repulsão) em uma separação de um comprimento de onda de Compton, e o resto de energia da carga. É dada por α ≈ 6997729735300000000♠7.297353×10⁻³, que é aproximadamente igual a 1137.^[69]

Quando elétrons e pósitrons colidem, eles se aniquilam, dando origem a dois ou mais fótons de raios gama. Se o elétron e o positron tem um momento desprezível, um positrônio pode se formar antes do evento de aniquilação em dois ou três fótons de raios gama totalizando 1.022 MeV.^[102][103] Por outro lado, fótons de energia elevada podem se transformar em um elétron e um pósitron num processo chamado de produção de par, mas somente na presença de um partícula carregada próxima, tal como um núcleo.^[104][105]

Na teoria da interação eletrofraca, o componente canhoto da função de onda do elétron forma um isospin fraco pareado com um elétron neutrino. Isto significa que durante a interação fraca, elétrons neutrinos se comportam como elétrons. Ambos os membros deste par suportam uma interação de corrente carregada pela emissão ou absorção de um W e pode ser convertida em um outro membro. A carga é conservada durante a reação porque o bóson W também carrega uma carga, cancelando qualquer mudança líquida durante a transmutação. Interações de correntes carregadas são responsáveis pelo fenômeno de decaimento beta em um átomo radioativo. O elétron e o elétron neutrino podem suportar uma interação de corrente neutra pela troca de um Z0
, e isto é responsável pela dispersão elástica do elétron neutrino.^[106]

Átomos e moléculas |

Função densidade de probabilidade para os primeiros orbitais do átomo de hidrogênio, vistos em seção transversal. O nível de energia para a ligação do elétron determina o orbital que ocupa, e a cor reflete a probabilidade de encontrar um elétron em determinada posição.

Um elétron pode se ligar ao núcleo de um átomo pela atração da força de Coulomb. Um sistema com um ou mais elétrons conectado a um núcleo é denominado átomo. Se o número de elétrons for diferente da carga elétrica do núcleo, tal átomo é denominado íon. O comportamento similar a onda de uma ligação eletrônica é descrita por uma função denominada orbital atômico. Cada orbital tem seu próprio conjunto de números quânticos tais como energia, momento angular e projeção do momento angular, e somente um conjunto distinto desses orbitais existe em volta do núcleo. De acordo com o princípio da exclusão de Pauli, cada orbital deve ser ocupado por até dois elétrons, que devem diferir em seu número quântico de spin.

Os elétrons podem se transferir entre orbitais diferentes por meio da emissão ou absorção de um fóton cuja energia é igual à diferença das energias inicial e final.^[107] Outros métodos de transferência de orbital incluem colisões com partículas, tais como o que ocorre no efeito Auger.^[108] Para escapar de um átomo, a energia do elétron deve ser superior à energia de ionização daquele átomo. Isto ocorre, por exemplo, com o efeito fotoelétrico, quando a energia de um fóton que colide com um átomo é maior do que a energia de ionização daquele átomo.^[109]

O momento angular do orbital é quantizado. Por possuir carga, o elétron produz um momento magnético orbital que é proporcional ao seu momento angular. O momento magnético líquido de um átomo é igual à soma vetorial do momento angular orbital e dos momentos magnéticos de spin de todos os elétrons e do núcleo. O momento magnético do núcleo é desprezível comparado com o dos elétrons, que ao ocupar o mesmo orbital (denominados, elétrons emparelhados) se cancelam.^{[necessário esclarecer][110]}

As ligações químicas entre átomos ocorrem como resultado da interação eletromagnética, conforme descrita pelas leis da mecânica quântica.^[111] A ligação mais forte é formada pelo compartilhamento ou transferência de elétrons entre átomos, permitindo a formação de moléculas.^[12] Dentro da molécula, os elétrons de movem sob a influência de vários núcleos atômicos, ocupando um orbital molecular; tanto como podem ocupar orbitais atômicos de átomos isolados.^[112] Um fator fundamental nestas estruturas moleculares é a existência de pares de elétrons. Estes são elétrons com spins opostos, permitindo a estes ocupar o mesmo orbital molecular sem violar o princípio da exclusão de Pauli (tal como no átomo). Orbitais moleculares diferentes tem distribuição espacial diferentes da densidade dos elétrons. Por exemplo, em pares ligados (i.e. em que os pares estão conectados os átomos) os elétrons podem ser encontrados com a probabilidade máxima em um volume relativamente pequeno entre os núcleos. Por outro lado, em pares de elétrons não ligados estes estão distribuídos ao largo de um grande volume ao redor do núcleo.^[113]

Condutividade |

Um raio consiste basicamente de uma descarga de elétrons.^[114] O potencial elétrico necessário para um raio pode ser gerado pelo efeito triboelétrico.^[115][116]

Se um corpo tem mais ou menos elétrons do que o necessário para balancear a carga positiva de seu núcleo, então o objeto tem uma carga elétrica líquida. Quando existe um excesso de elétrons, é dito que está carregado negativamente. Quando existem menos elétrons do que o número de prótons no núcleo, é dito que está carregado positivamente. Quando o número de elétrons e prótons é igual, suas cargas se cancelam e o objeto está neutro eletricamente. Um corpo macroscópico pode desenvolver uma carga elétrica pela fricção e pelo efeito triboelétrico.^[117]

Elétrons independentes se movendo no vácuo são denominados livres. Em metais, também se comportam como se fossem livres. Na realidade as partículas que são comumente chamadas de elétrons nos metais e outros sólidos são quase-elétrons-quasipartículas, que têm a mesma carga elétrica, spin e momento magnético de um elétron real mas podem possuir uma massa diferente.^[118]

Quando elétrons livres -tanto no vácuo quanto em metais- se movem, produzem uma rede de fluxo de carga denominada corrente elétrica, que gera um campo magnético. Do mesmo modo uma corrente pode ser criada por uma mudança no campo magnético. Estas interações são descritas matematicamente pela equação de Maxwell.^[119]
Em uma dada temperatura, cada material tem uma condutividade elétrica que determina o valor da corrente elétrica quando um potencial elétrico é aplicado. Exemplos de bons condutores incluem metais tais como o cobre e o ouro, enquanto que o vidro e o Teflon são péssimos condutores. Em qualquer material dielétrico, os elétrons permanecem conectados aos seus respectivos átomos e o material se comporta como um isolante elétrico. A maioria dos semicondutores tem um nível variável de condutividade que reside entre os extremos de condução e isolamento elétrico.^[120] Por outro lado, metais têm uma estrutura eletrônica de banda contendo bandas eletrônicas parcialmente preenchidas. A presença de tais bandas permite que os elétrons em metais se comportem como se fossem livres ou deslocalizados. Estes elétrons não estão associados a um átomo específico, então quando um campo elétrico é aplicado, eles ficam livres para se mover como um gás (denominado gás de Fermi)^[121] através do material como se fossem elétrons livres.

Por causa da colisão entre átomos e elétrons, a velocidade de deriva dos elétrons em um condutor é da ordem de milímetros por segundo. Todavia, a velocidade em que a mudança de corrente em um ponto do material causa mudanças de corrente em outras partes do material, a velocidade de propagação, é aproximadamente 75% da velocidade da luz.^[122] Isto ocorre porque sinais elétricos se propagam como uma onda, com a velocidade dependente da constante dielétrica do material.^[123]
Metais são relativamente bons condutores de calor, basicamente por conta dos elétrons deslocalizados que são livres para transportar energia térmica entre átomos. Porém, ao contrário da condutividade elétrica, a condutividade térmica é quase independente da temperatura. Isto é expresso matematicamente pela lei de Wiedemann–Franz,^[121] que expressa que a relação da condutividade térmica para a elétrica é proporcional a temperatura. A desordem térmica na treliça metálica aumenta a resistividade elétrica do material, produzindo uma dependência da temperatura para a corrente elétrica.^[124]
Quando resfriados a um ponto denominado temperatura crítica, materiais podem ser submetidos a uma transição de fase em que perdem toda a resistividade a corrente elétrica, em um processo conhecido como supercondutividade. Na teoria BCS, este comportamento é modelado por pares de elétrons entrando num estado quântico chamado de condensado de Bose-Einstein. Este par de Cooper tem seus movimentos acoplados a matéria próxima via vibrações na rede chamadas de fônons, e por meio disso evitam as colisões com átomos que normalmente criam a resistência elétrica.^[125] (Pares de Cooper tem um raio de aproximadamente 100 nm, portanto podem se sobrepor uns aos outros.)^[126] Entretanto, o mecanismo pelo qual supercondutores de temperatura superior operam ainda permanece incerto.

Elétrons no interior de sólidos condutores, nos quais são quasipartículas, quando confinados firmemente em temperaturas próximas ao zero absoluto, se comportam como se tivessem divididos em três outras quasipartículas: spínons, órbitons e hólons.^[127][128] O primeiro carrega o spin e momento magnético, o segundo a localização orbital e o último a carga.

Movimento e energia |

De acordo com a teoria da relatividade especial de Einstein, a medida que um elétron se aproxima da velocidade da luz, do ponto de vista de um observador sua massa relativística aumenta, e por causa disso torna-se mais difícil acelerar a partir de dentro do plano do observador de referência. A velocidade do elétron pode se aproximar, mas nunca alcançar, a velocidade da luz no vácuo, c. Entretanto, quando elétrons relativísticos- isto é, elétrons se movendo a uma velocidade próxima de c-são injetados em um meio dielétrico tal como a água, onde a velocidade local da luz é significantemente menor que c, os elétrons temporariamente se movem mais rápido do que a luz no meio. A medida que interagem com o meio, eles geral uma luz fraca denominada radiação Cherenkov.^[129]

Fator de Lorentz em função da velocidade. Inicia com o valor 1 e tende ao infinito a medida que v se aproxima de c.

Os efeitos da relatividade especial são baseados em uma quantidade conhecida como fator de Lorentz definido como γ=1/1−v2/c2{displaystyle scriptstyle gamma =1/{sqrt {1-{v^{2}}/{c^{2}}}}} onde ‘’v’’ é a velocidade da partícula. A energia cinética K_e de um elétron se movendo com velocidade v é:

Ke=(γ−1)mec2,{displaystyle displaystyle K_{mathrm {e} }=(gamma -1)m_{mathrm {e} }c^{2},}

onde m_e é a massa do elétron. Por exemplo, o Centro Acelerador Linear de Stanford pode acelerar um elétron a aproximadamente 51 GeV.^[130]
Uma vez que um elétron se comporta como um onda, em uma dada velocidade tem a característica do comprimento de onda de Broglie. Isto é dado por λ_e = h/p onde h é a constante de Planck e p é o momento.^[52] Para o elétron de 51 GeV acima, o comprimento de onda é aproximadamente 6983240000000000000♠2.4×10⁻¹⁷ m, que é pequeno o suficiente para explorar estruturas inferiores ao tamanho do núcleo atômico.^[131]

Formação |

Produção de par provocada pela colisão de um fóton com um núcleo atômico

A teoria do Big Bang é amplamente aceita para explicar os estágios iniciais da evolução do Universo.^[132] Durante o primeiro milissegundo do Big Bang, a temperatura era superior a 10 bilhões Kelvin e os fótons tinham energia media superior a milhares de elétron-volts. Estes fótons tinham energia suficiente para reagir um com outro para formar pares de elétrons e pósitrons. Da mesma forma, os pares de elétron-pósitron se aniquilavam e emitiam fótons energéticos:

γ + γ ↔ e+
+ e−

Um equilíbrio entre elétrons, pósitrons e fótons foi mantido durante esta fase da evolução do Universo. Porém, após 15 segundos terem se passado, a temperatura do universo caiu a um limiar inferior onde a formação elétron-pósitron poderia ocorrer. A maior parte dos elétrons e pósitrons sobreviventes se aniquilou, liberando radiação gama que reaqueceu o universo.^[133]

Por razões que permanecem incertas, durante o processo de leptogênese havia um excesso no número de elétrons em relação aos pósitrons.^[134] Assim, aproximadamente um elétron a cada bilhão sobreviveu ao processo de aniquilação. Este excesso foi compatível com o excesso de prótons em relação aos antiprótons, em uma condição conhecida como assimetria bárion, que resultou em uma carga líquida de zero para o universo.^[135][136] Os prótons e nêutrons remanescentes começaram a participar de reações em um processo conhecido como nucleossíntese, formando isótopos do hidrogênio e hélio, com traços do elemento lítio. Este processo atingiu um máximo após aproximadamente cinco minutos.^[137] Os nêutrons remanescentes da nucleossíntese passaram por um decaimento beta negativo com uma meia-vida de aproximadamente mil segundos, liberando um próton e um elétron no processo,

n → p + e−
+ ν
e

Pelos próximos 7005300000000000000♠300000–7005400000000000000♠400000 anos, o excesso de elétrons permaneceu com muita energia para se conectar ao núcleo atômico.^[138] O que se seguiu foi um período conhecido como recombinação, quando os átomos neutros foram formados e o universo em expansão se tornou transparente para a radiação.^[139]

Aproximadamente um milhão de anos após o big bang, a primeira geração de estrelas começou a se formar.^[139] No interior da estrela, a nucleossíntese estelar resultou na produção de pósitrons da fusão do núcleo atômico. Estas partículas de antimatéria imediatamente aniquilaram os elétrons, liberando raios gama. O resultado foi uma redução estável no número de elétrons, e um aumento compatível no número de nêutrons. Todavia, o processo de evolução estelar pode resultar na síntese de isótopos radioativos. Alguns isótopos podem subsequentemente passar por um decaimento beta negativo, emitindo um elétron e um antineutrino do núcleo.^[140] Um exemplo é o isótopo Cobalto-60 (⁶⁰Co) que decai para formar o Níquel-60.^[141]

Processo de produção de partículas geradas por um raio cósmico energético que atinge a atmosfera terrestre

No final de sua vida, uma estrela com mais de 20 massas solares pode passar por um colapso gravitacional para formar um buraco negro.^[142] De acordo com a física clássica, estes objetos estelares massivos exercem uma atração gravitacional tão forte que previnem qualquer coisa, até mesmo a radiação eletromagnética, de escapar do raio de Schwarzschild. Porém, acredita-se que os efeitos da mecânica quântica potencialmente permitem a emissão da radiação de Hawking a esta distância. Presume-se que elétrons e pósitrons são criados no horizonte de eventos destas estrelas restantes.

Quando pares de partículas virtuais (tal como um elétron e um pósitron) são criados nas proximidades do horizonte de eventos, a distribuição especial aleatória destas partículas pode permitir a um deles aparecer no exterior; este processo é denominado tunelamento quântico. O potencial gravitacional do buraco negro pode fornecer a energia necessária para transformar esta partícula virtual em uma real, permitindo ser irradiada para o espaço.^[143] Em compensação, o outro membro do par é dado uma energia negativa, que resulta em uma perda líquida de energia-massa pelo buraco negro. A taxa de aumento da radiação de Hawking aumenta com o decréscimo da massa, eventualmente causando a evaporação do buraco negro até, finalmente, explodir.^[144]

Raios cósmicos são partículas viajando através do espaço com energias elevadas, com registros de valor tão altos quanto 7001480652946100000♠3.0×10²⁰ eV.^[145] Quando estas partículas colidem com núcleos atômicos na atmosfera terrestre, uma chuva de partículas é gerada, incluindo píons. ^[146] Mais da metade da radiação cósmica observada na superfície da terra consiste de múons. Esta partícula é um lépton produzido na atomosfera superior pelo decaimento de um píon.

π−
→ μ−
+ ν
μ

Um múon, por sua vez, pode decair para formar um elétron ou um pósitron.^[147]

μ−
→ e−
+ ν
e + ν
μ

Observação |

Aurora polar são causadas principalmente por elétrons energizados precipitando na atmosfera.^[148]

A observação remota de elétrons requer a detecção das suas energias radiadas. Por exemplo, em ambientes altamente energizados como a coroa solar, elétrons livres formam o plasma que irradia energia devido a radiação Bremsstrahlung. O gás de elétron pode ser submetido a oscilação plasmática, que são ondas provocadas por variações sincronizadas na densidade do elétron, e estes produzem emissões energéticas que podem ser detectadas por radiotelescópios.^[149]

A frequência de um fóton é proporcional a sua energia. Conforme um elétron transita entre diferentes níveis de energia em um átomo, absorve ou emite um fóton em uma frequência característica. Por exemplo, quando átomos são irradiados por uma fonte de espectro amplo, surgem linhas de absorção distintas no espectro da radiação transmitida. Cada elemento ou molécula demonstra um conjunto característico de linhas espectrais, tal como o espectro do átomo de hidrogênio. Medições espectroscópicas da intensidade e tamanho destas linhas permitem determinar a composição e propriedades físicas da substância.^[150][151]

Em condições de laboratório, a interação de elétrons individuais pode ser observada por meio de um detector de partícula, que permite a medição de propriedades específicas tais como energia, spin e carga.^[109] O desenvolvimento da armadilha de íons quadrupolo e a armadilha de Penning permitiu que partículas carregadas fossem contidas em regiões pequenas por períodos longos. Isto permitiu a medição precisa das propriedades das partículas. Por exemplo, em uma ocasião a armadilha de Penning foi utilizada para conter um único elétron por um período de dez meses. ^[152] O momento magnético do elétron foi medido com uma precisão de onze dígitos, que, em 1980, era superior a qualquer outra constante física.^[153]

O primeiro vídeo com imagens da distribuição energética de um elétron foi gravado por uma equipe da Universidade de Lund, Suécia, em fevereiro de 2008. Os cientistas utilizaram flashes luminosos extremamente curtos, chamados pulsos de attosegundos, que permitiram a observação do elétron pela primeira vez. ^[154][155]

A distribuição de elétrons em materiais sólidos pode ser visualizada pela espectroscopia de fotoemissão angular (ARPES). Esta técnica emprega o efeito fotoelétrico para medir o espaço recíproco- uma representação matemática de estruturas periódicas que é utilizada para inferir a estrutura original. A ARPES pode ser usada para determinar a direção, velocidade e dispersão do elétron dentro do material.^[156]

Aplicações em plasma |

Feixes de partículas |

Durante um teste no túnel de vento da NASA, um modelo do ônibus espacial é bombardeado com um feixe de elétrons, simulando o efeito dos gases ionizantes durante a reentrada.^[157]

Feixes de elétrons são utilizados na soldagem. ^[158] Eles permitem densidades energéticas de até 7007100000000000000♠10⁷ W·cm⁻² ao longo de um diâmetro focal de 0.1–1.3 mm e normalmente não requerem material de preenchimento. Esta técnica de soldagem precisa ser executada no vácuo para prevenir que os elétrons interajam com os gases antes de atingir seu alvo, e pode ser usada para unir materiais condutivos que seriam incompatíveis para soldagem por outros métodos.^[159][160]

A litografia por feixe de elétrons é um método de gravação de semicondutores com resoluções menores que um micrômetro.^[161] Esta técnica é limitada pelo alto custo e baixa performance, a necessidade de operar o feixe no vácuo e a tendência dos elétrons se dissiparem no sólido. O último problema limita a uma resolução de 10 nm. Por esta razão, só é utilizada para a produção de um pequeno número de circuitos integrados especializados.^[162]

A irradiação por elétrons é utilizada em materiais para mudar suas propriedades físicas ou esterilizar produtos alimentícios e médicos.^[163] O feixe de elétrons torna-se fluido ou quase derrete o vidro sem incremento significativo da temperatura ou intensidade da radiação: e.g. a radiação intensiva de elétrons causa a diminuição de em muitas ordens de magnitude da viscosidade e diminuição gradual de sua energia de ativação.^[164]

Os aceleradores de partículas lineares geram feixes de elétrons para o tratamento de tumores superficiais na radioterapia. Esta técnica pode ser usada para tratamento de lesões de pele como o carcinoma basocelular porque o feixe de elétron tem uma baia penetração antes de ser absorvido, normalmente até 5 cm para elétrons energizados na faixa de 5–20 MeV. Um feixe de elétrons pode ser usado para suplementar o tratamento de áreas que têm sido irradiadas por raio-x.^[165][166]

Os aceleradores de partículas usam campos elétricos para impulsionar elétrons e suas antipartículas para energias elevadas. Estas partículas emitem radiação sincrotrônicas conforme passam pelo campo magnético. A dependência da intensidade desta radiação sobre o spin polariza o feixe de elétrons- um processo conhecido como efeito Sokolov–Ternov.^{[notas 9]} Feixes de elétrons polarizados podem ser úteis para vários experimentos. A radiação sincrotrônica também pode resfriar o feixe de elétrons para reduzir a difusão do momento das partículas. Feixes de elétrons e pósitrons são colididos com as partículas acelerando na energia requerida; detectores de partículas observam a emissão energética resultante, que a física de partículas estuda.^[167]

Imagiologia |

A difração de elétrons de baixa energia é um método de bombardear um material cristalino com um feixe de elétrons alinhado e então observar o padrão de difração resultante para determinar a estrutura do material. É requerida uma energia na faixa de 20–200 eV.^[168] A técnica de difração de elétrons de alta energia usa a reflexão de um feixe de elétrons disparado em vários ângulos pequenos para caracterizar a superfície do material cristalino. O feixe de energia normalmente está na faixa de 8–20 keV e o ângulo de incidência é de 1–4°.^[169][170]

A microscopia eletrônica direciona um feixe de elétrons sobre o espécime. Alguns elétrons mudam suas propriedades, tais como a direção do movimento, ângulo, e energia e fase relativa conforme interagem com o material. Os microscopistas podem registrar estas mudanças no feixe de elétrons e reproduzir imagens de nível atômico do material.^[171] Sob luz azul, a microscopia ótica convencional tem uma resolução de difração limitada a aproximadamente 200 nm.^[172] Em comparação, a microscopia eletrônica é limitada ao comprimento de onda de Broglie do elétron, que é igual a 0.0037 nm para partículas aceleradas através de um potencial de 100.000-Volts.^[173] O Microscópio eletrônico de transmissão de aberração corrigida é capaz de atingir uma resolução inferior a 0.05 nm, que é mais do que suficiente para visualizar átomos individualmente.^[174] Esta capacidade torna a microscopia eletrônica útil para a imagiologia de alta resolução. Entretanto, são instrumentos caros com alto custo de manutenção.

Existem dois tipos de microscópios eletrônicos: por transmissão ou por varredura. O microscópio eletrônico de transmissão funcionam como um retroprojetor, com o feixe de elétrons passando através de uma fatia do material e sendo projetadas por lentes em um slide fotográfico ou dispositivo de carga acoplada. O microscópio eletrônico por varredura emitem um feixe de elétrons fino, assim como em um aparelho de TV, através da amostra analisada para reproduzir a imagem. A faixa de ampliação vai de 100× até 1.000.000× ou superior para ambos os tipos. O microscópio de corrente de tunelamento utiliza tunelamento quântico de elétrons a partir de uma ponta de metal afiada para dentro do material estudado e pode produzir imagens a nível atômico da superfície.^{[175][176][177]}

Outras aplicações |

No laser de elétrons livres, um feixe de elétrons relativísticos passa através de um par de onduladores que contém uma matriz de imãs dipolares cujos campos apontam em direções alternadas. Os elétrons emitem radiação sincrotrônica que interage de forma coerente com os mesmos elétrons para amplificar o campo de radiação na frequência de ressonância. O laser pode emitir radiação eletromagnética de radiança coerente em uma faixa ampla de frequências, desde o microondas até o raio-X.^[178]

Os elétrons são importantes em tubos de raios catódicos, onde têm sido amplamente utilizados em dispositivos de imagem em instrumentos de laboratório, monitores de computador e aparelhos de televisão.^[179] Em um tubo fotomultiplicador, cada fóton que atinge o fotocátodo inicia uma avalanche de elétrons que produz um pulso de corrente detectável.^[180] Tubos de vácuo utilizam um fluxo de elétrons para manipular sinais elétricos, e possuem um papel crítico no desenvolvimento da tecnologia eletrônica. Porém, eles têm sido substituídos por dispositivos de estado sólido tais como transistores.^[181]

Ver também |

Notas

Referências

Ligações externas |

O Wikcionário tem o verbete Elétron.

• 
  The Review of Particle Physics (em inglês) no Particle Data Group


• 
  O experimento de Millikanno e-Química

• Portal da ciência
• Portal da física